4.1 Video Motion Analysis using “Tracker”
Paste screen captures here with the following graphs for each of the 3 trials:
*Due to the field of vision from the filming position provided, the camera is unable to capture the entire journey travelled by the car. Thus, the graphs are inaccurate, however, similar.
- Displacement – time graph
Trial 1
Trial 2
Trial 3
- Velocity – time graph
Trial 1
Trial 2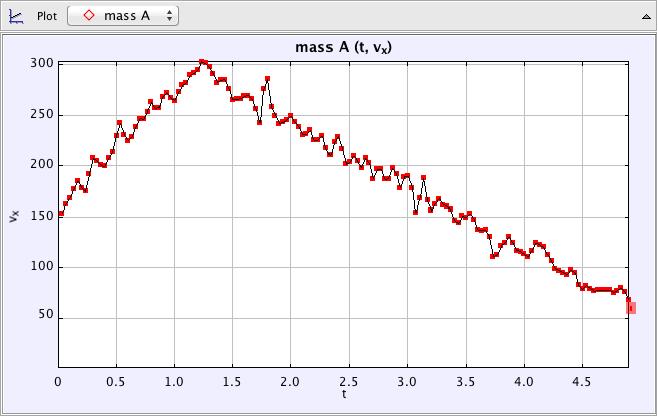
Trial 3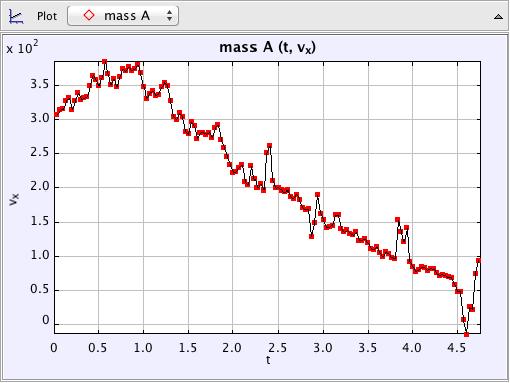
- Acceleration – time graph
Trial 1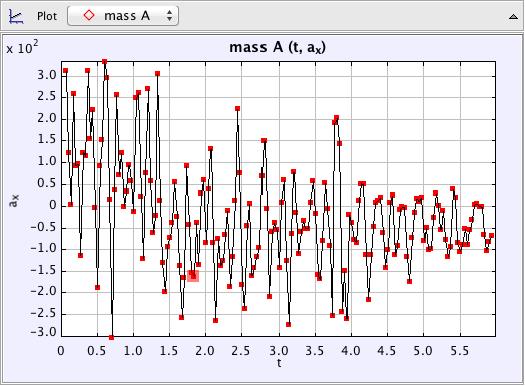
Trial 2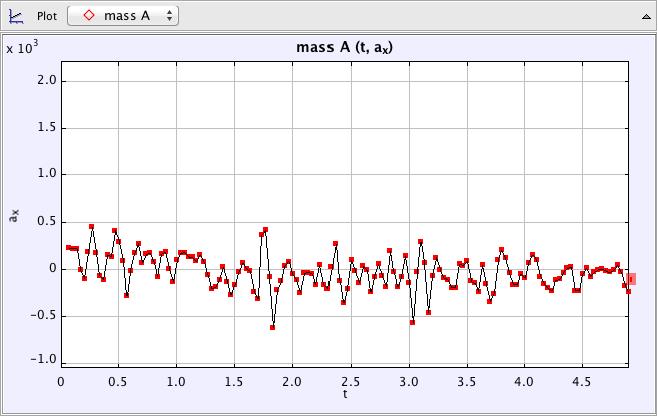
Trial 3
4.2 Data Analysis
- Which wheels are you drive wheels? (front or back)
Back wheels
- What is the circumference of your drive wheels?
37.7cm
- How far will your car travel in one rotation of the drive wheels?
37.7cm
- How many rotations (on average ) were there in each run?
24
- How much string is used in one rotation of the drive wheels? Show how you calculated this.
String used in one rotation of the drive wheel = Circumference of the axle = 4.08cm (3sf)
- The release of the lever is the power stroke. What is the length of your vehicles power stroke? (Length of string released)
47cm
- Calculate how far your vehicle will travel during the power stroke. Show your calculations!!
Number of round of coils x Circumference of wheel = Distance car will travel during power stroke
9 x 37.7 = 339 cm
= 3.39m (3sf)
- Compare the answer to #7 to the distance your measured during your car’s power stroke. Discuss possible reasons for different valuables.
The distance measured during our car’s power stroke differed a lot from our answer to #7.
During the calculation, we did not take into account the presence of friction and air resistance, hence, the results are different.
- Calculate the average velocity for your car during the period after the spring fully releases.
Average distance the car travels according to the 3 trials = 9m
Average velocity after the spring fully releases = (9m-3.39m)/(7.1s-2s) = 1.1m/s
- What force causes your car to stop?
Friction and air resistance.
- The work done by a force is calculated by multiplying the force times the distance over which it acts. The work done on an object is equal to the change in its kinetic energy. Can you find a way to calculate the force of friction? Use equations and explain your steps. HINT: Be careful, you have calculated average velocity. How can you find the total amount of kinetic energy (immediately after spring release) if we assume the acceleration during coasting was constant?
Assume the car has no friction,
KE = ½ * m * v^2
= ½ * 0.326 x 1.1
= 0.179 J (3sf)
Let Fa = Applied force
Fa = m x a
= 0.326 x 0.1
= 0.0326 N
Let Work done = KEw
Let d = distance travelled by the car after string releases
KEw = 0.0326 x 5.61
= 0.163 J (3sf)
Let KEf = Work done by friction
KEf = KE - KEw
= 0.179 - 0.163
= 0.016 J
Friction = KEf/d
= 0.016/5.61
= 0.00285 N (3sf)
- Various experiments have been done to measure the potential energy available from the spring. One estimate is 0.65 Joules. Using your estimates of the maximum kinetic energy of your car and the work done by friction, discuss whether or not this is a reasonable value. Can you account for any differences in the forms of energy? You must justify all of your arguments.
No, this is not a reasonable value. By comparing the calculated maximum kinetic energy of our car (0.179J), the estimated potential energy has a difference of 0.471 J. This difference can make a great difference in the performance of the car as there is more energy provided for a greater speed and distance of the car despite the friction generated from the uncoiling of the string. The friction generated by the roughness of the string would affect the potential energy converted to kinetic energy of the car as potential energy would also be converted to other forms of energy such as heat and sound energy. Hence, the estimate would be inaccurate.
No comments:
Post a Comment